Logaritmické pravítko se skládá za tří částí:
- pevná část (základní) složená ze dvou běhounů opatřených drážkami, ve kterých se pohybuje střední část pravítka (šoupátko)
- šoupátko (pohyblivá část), která se posunuje v drážkách pevné části
- průhledný jezdec (kurzor) s jednou nebo několika ryskami (indexy)
Na obrázku 5″ pravítka Logarex 27103 se pod kurzorem myši zobrazí název vybrané části.
Podle uspořádání pevné části se rozlišují dva typy:
- uzavřený, kdy má pravítko horní a spodní běhoun mezi sebou propojené v celé délce a v tomto případě je pravítko opatřené stupnicemi jen na jedné – lícové straně
- otevřený, kdy jsou běhouny propojené jen na okrajích, a to umožňuje, aby mohlo být pravítko oboustranné a opatřené stupnicemi i na rubové straně
Pevná část logarimického pravítka i jeho šoupátko jsou opatřeny několika stupnicemi. Podle jejich uspořádání rozlišujeme několik typů pravítek. Popíšeme si je na nejčastějším a poměrně jednoduchém typu označovaném jako Reitz. Jedná se o 5″ model Faber Castell 67/87. Začneme shora:
- na sešikmené hraně pevné části je rovnoměrná pravítková stupnice v centimetrech
- další stupnicí je kubická, představující x³ a označovaná K
- následují shodné kvadratické stupnice A na pevné části a B na šoupátku, které reprezentují x²
- střední stupnice na šoupátku je reciproká, označovaná CI nebo R a představující 1/x
- další dvě shodné stupnice označené C na šoupátku a D na pevné části reprezentují hodnotu x
- poslední stupnicí na líci je základní logaritmická stupnice označená L a představující log x
- na spodní hraně pak bývá stupnice v měřítku 1:25 nebo na některých modelech stupnice v coulech
Na rubové straně šoupátka jsou pak stupnice označené S, ST a T reprezentující sin x, sin/tg x a tg x.
Pro popis stupnic se používá symbolické značení, které by pro naše pravítko vypadalo takto:
líc: 14cm // K, A [ B, CI, C ] D, L
rub: [ S, ST, T ]
Symbolické pojmenování stupnic
Pojmenování stupnic logaritmického pravítka byl pravděpodobně největší konstrukční úlet na jinak naprosto úžasném díle. Dávalo by jistě mnohem větší smysl pojmenovat stupnice podle jejich významu, tedy například x, 1/x, x², x³ a podobně. A stupnice některých pravítek jsou takto označovány. Z důvodů ztracených v historii ale vznikl obecný úzus označovat stupnice písmeny, bez jakéhokoli významu a tak jsou základní stupnice označeny písmeny A, B, C a D. Je pravděpodobné, že důvodem bylo usnadnění při tvorbě instrukcí v uživatelské dokumentaci. Těžko by se popisoval postup, jestliže by stupnice nebyly označeny vůbec. A tak vzniklo zřejmě symbolické označení, které v některých případech ani nekoresponduje s významem stupnice. Mnoho výrobců přidalo na pravou stranu stupnic jejich přirozené pojmenování (x, 1/x, atd) a levou stranu ponechalo vyhrazenou pro obecně používaný symbolický název. Některé, zejména severoamerické firmy však měly pocit, že člověk schopný používat logaritmické pravítko pomoc v podobě označování stupnic nepotřebuje a uživatelsky přívětivým značením stupnic se moc nezbývaly.
| Označení stupnice | Hodnota (vztažená ke stupnici C nebo D) | Popis použití |
|---|---|---|
| A | x² | Kvadratická stupnice. Typicky se nachází na horní pevné části pravítka a používá se ve spojení se stupnicí D ze spodní pevné části pravítka. Druhou mocninu hodnoty ze stupnice A odečteme právě na stupnici A a naopak, druhou odmocninu hodnoty ze stupnice A nalezneme na stupnici D. V tomto druhém případě je nutné vzít v úvahu počet číslic, abychom použili správnou část stupnice A (porovnejte se stupnicí R1/R2 níže). Stupnice má typicky hodnoty od 1 do 100. |
| B | x² | Kvadratická stupnice. Nalézá se na pohyblivém šoupátku a používá se ve spojení se stupnicí C opět pro odečet druhé mocniny/odmocniny obdobně jako dvojice stupnic A/D. |
| C | x | Základní stupnice logaritmického pravítka. Nachází se na pohyblivé části (šoupátku) pravítka a většina výpočtů probíhá s využitím základních stupnic C/D scales. Obsahuje hodnoty od 1 do 10 (nebo od 0.1 do 1, nebo od 10 do 100, atd. v závislosti na potřebě) ve formátu základní logaritmické stupnice. Na některých pravítkách bývá stupnice rozšířena ještě pod hodnotu 1 a nad hodnotu 10 pro usnadnění některých výpočtů. |
| CF | x × π | Složená stupnice C obvykle začínající na hodnotě π (tj 3,14159...). Používá se pro rychlé násobení nebo dělení při řešení úloh s hodnotou π. Nachází se na šoupátku (pohyblivé části) a je vhodná pro výpočty zahrnující kružnice a koule, chceme-li se vyhnout nutnosti přesouvat průhledný jezdec. Tato stupnice se obvykle nachází na duplexních pravítkách. |
| CF/M | x × loge10 | Složená stupnice C obvykle začínající hodnotou 2,302585, což je logaritmus čísla 10 při základu e (přirozený logaritmus, někdy také Napierův). Tato složená stupnice umožňuje rychlé převádění výsledky logaritmů ze základu 10 do základu e. Stupnice bývá většinou jen na nejvyšších modelech logaritmických pravítek. |
| CI | 1 / x | Převrácená stupnice C, která obsahuje převrácenou hodnotu C (stupnice je sestupná, tedy od 10 k 1 a je nutno ji takto číst). Nachází se na šoupátku (pohyblivé části) a je vhodná pro zjednodušení dělení nebo násobení. |
| CIF | 1 / x × π | Převrácená složená stupnice C s převrácenými hodnotami stupnice CF. Bývá umístěna na šoupátku (pohyblivé části) a typicky ji obsahují jen nejvyšší modely logaritmických pravítek. Používá se pro výpočty zahrnující hodnotu π. |
| D | x | Základní stupnice logaritmického pravítka. Nachází se na pevné části pravítka a většina výpočtů probíhá s využitím základních stupnic C/D. Obdobně jako stupnice C pokrývá hodnoty typicky od 1 do 10, s možným rozšířením pod a nad tyto hodnoty pro usnadnění někreých výpočtů. |
| DF | x × π | Složená stupnice D je identická se stupnicí CF. Obvykle začíná na hodnotě π a je umístěna na pevné části logaritmického pravítka. Bývá na duplexních pravítkách a používá se pro řešení úloh s hodnotou π. |
| K | x³ | Kubická stupnice se nachází na pevné části logaritmického pravítka. Používá se ve spojení se stupnicí D pro určení třetí mocniny a odmocniny. Mívá rozsah od 1 do 1000. Běžně se vyskytuje na většině pravítek. Při výpočtech zejména třetí odmocniny je třeba si dávat pozor na počet číslic. |
| P | √(1-x²) | Pythagorova stupnice bývá umístěna na pevné části logaritmického pravítka. Používá se pro přesnější stanovení cos ze sin (S) pro malé úhly. Lze ji použít také pro výpočet druhé odmocniny (1-x²) ve spojení se stupnicemi D a A. Typicky bývá na pravítkách systému Darmstadt. Hodnota obvykle bývá od 0,995 do 0. |
| S | sin x | Stupnice sinus a cosinus se používá k určení sin nebo cos úhlu, typicky v rozmezí od 5,7 do 90 stupňů (existují určité rozdíly ve spodní hranici). Často bývají na jedné stupnici rostoucí čísla sin a klesající čísla cos. Stupnice mívá rozmezí hodnot od 0,1 do 1,0 a používá se ve spojení se stupnicemi C a D. Tato stupnice bývá na většině logaritmockých pravítek. |
| ST | sin, tg x | Stupnice sinus a tangens je rozšířením stupnice S pro malé úhly typicky v rozmezí od 0,57 do 5,7 stupňů (existují určité rozdíly ve spodní hranici i horní hranici). Protože sin a tg nabývají v tomto rozmezí téměř stejných hodnot, bývají umístěny na jediné stupnici. Stupnice mívá rozmezí hodnot od 0,01 do 0,1 a používá se ve spojení se stupnicemi C a D. Tato stupnice bývá na většině logaritmockých pravítek. |
| T | tg, cotg x | Stupnice tangens a cotangens se používá k určení tg nebo cotg úhlu, typicky v rozmezí od 5,7 do 45 stupňů na jednoduchých pravítkách případně až do 84,5 stupně na vyšších modelech. Základní rozsah do 45 stupňů se používá ve spojení se stupnicemi C nebo D a od 45 do 84,5 stupně ve spojení se stupnicí CI. |
Standardní uspořádání stupnic
V následujícím přehledu se pokusím popsat základní typy logaritmických pravítek. Někteří z Vás si možná budou pamatovat klasická logára ve tvaru pravítka, jenže ono jich bylo více tvarů – také kruhová, válcová. Ale začněme od těch lineárních. Při popisu stupnic budu postupovat shora dolů. Ostré závorky [ ] uvozují pohyblivou část pravítka.
Lineární
Mannheim
Líc: A [ B, CI, C ] D, K
Rub: [ S, L, T ]
Původně logaritmická pravítka obsahovaly jen stupnice A, B, C, D. Většina modernějších verzí přidala také inverzní C stupnici CI na lícové straně šoupátka a kubickou stupnici K na pevné části. Na rubové straně šoupátka obvykle naleznete stupnici sinusovou (S), tangenciální (T) a logaritmickou (L). Na obrázku je jednoduché 5″ anglické logaritmické pravítko Blundell 605. Podobně jako tento, i mnoho dalších modelů je vybaveno také palcovým nebo centimetrovým pravítkem.
Rietz
Líc: K, A [ B, CI, C ] D, L
Rub [S, ST, T ]
Toto uspořádání je obdobné, jako u uspořádání Mannheim, ale s několika rozdíly v umístění stupnic. Vpodstatě se jedná o logičtější uspořádání, kdy kubická stupnice (K) je umístěna nad kvadratickými stupnicemi A a B a logaritmická stupnice L je na lícové pevné části pravítka. Toto uspořádání umožnilo umístit na pohyblivou část rozšířenou sinusovou stupnici (ST) používanou jak pro sin, tak i tang. Na obrázku je 10″ československé pravítko Logarex 27401. Toto uspořádání je běžné pro většinu německých modelů. Modely jsou opět většinou doplněny centimetrovým nebo coulovým pravítkem.
Darmstadt
Líc: K, A [ B, CI, C ] D, P
Rub: [ LL1, LL2, LL3 ]
Systém Darmstadt je dalším německým vylepšením a velice populárním rozmístěním díky jeho všestranosti. Původní design Darmstadt přidával log-log stupnice na rub šoupátka a velmi užitečnou Pythagorejskou stupnici (P) na líci.
Existuje mnoho vylepšených alternativ tohoto uspořádání, kdy jsou například stupnice S a T přidány na pevnou část lícové strany a stupnice L a LL0 jsou umístěny na zadní straně šoupáta (na obrázku je 10″ československé pravítko Logarex 27403-X Darmstadt). Na toto uspořádání dále navazují oboustranné (duplexní) modely.
Oboustranné (Duplex) modely
Všechny oboustranné modely obsahují stupnice na obou starnách jak statické, tak pohyblivé části pravítka. Rovněž jezdec je oboustranný a umožňuje odkazovat mezi oběma stranami pravítka. Toto uspořádání dramticky zvětšuje počet stupnic a jejich kombinací, i když to může vést k větší chybovosti jednak ze záměny stupnic nebo z nechtěného pohybu během výpočtu. Uspořádání stupnic se významně liší model od modelu, ale některé charakteristiky jsou platné pro většinu modelů.
Většina pravítek obsahuje další log–log stupnice pro exponenciální výpočty (např. LL01, LL3), využívané pro řešení neceločíselných exponenciálních problémů. Obsahují také složené stupnice C/D s hodnotou π (tj vynásobené 3,14159…), které jsou velmi užitečné pro výpočty kružnic a koulí (např. CF, DF, CIF). Někteří výrobci také vybavili pravítka rozšířenými stupnicemi odmocnin, označovanými jako R1/R2 nebo Sq1/Sq2, nebo dalšími hyperbolickými stupnicemi (např. Sh1/Sh2, Th) na „vektorových“ modelech.
Variant řešení existuje nepřeberné množství a každý inklinuje k tomu svému nejoblíbenějšímu uspořádání nebo výrobci. Na obrázku je 10″ československý model Logarex 27602-II Exponent.
Kruhová
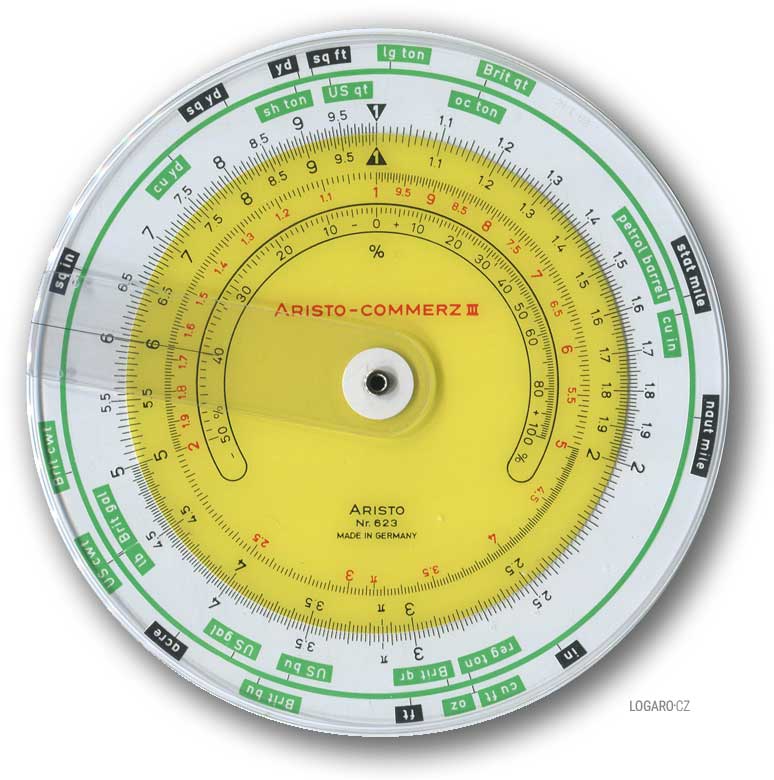
Kruhová logaritmická pravítka využívají výhody delších kruhových stupnic na omezeném prostoru. Využívají buď zdvojeného centrálně umístěného otočného jezdce nebo častěji druhého rotačního disku a jednoho jezdce, čímž se podobají lineárním pravítkům. Takovým příkladem může být Aristo 623. Kruhová logaritmická pravítka mohou být rovněž oboustranná. Nikdy nedosáhla popularity lineárních pravítek, možná kvůli problémům s udržením pozice jednotlivých pohyblivých dílů. Mezi kruhová pravítka se řadí také piloty používané letecká navigační pravítka.
Kapesní hodinky
Logaritmické pravítko ve tvaru kapesních hodinek je zmenšenou podobou kruhového logaritmického pravítka. Délkou stupnice se přibližují 10″ lineárnímu pravítku, ale kvůli omezenému prostoru nemohou obsahovat tolik stupnic. Na obrázku je ruské pravítko KL-1 (круговая линейка КЛ-1).
Válcová
Válcová pravítka jsou atraktivní především délkou stupnice a z toho vyplývající přesností.
Cylindrické
Typickým představitelem cylindrického logaritmického pravítka je anglický Otis King. Ve válci délky 17 cm a průměru 4 cm ve složeném stavu se skrývá stupnice dlouhá 1,68 m. Nevýhodou je, že stupnice je jediná a tím umožňuje jen násobení a dělení. Nicméně atraktivní design ho činí zajímavým sběratelským kouskem.
Na připojeném obrázku je Otis King model K 414/423.
Sudové
Sudové modely představují stolní logaritmická pravítka s velkou poskytovanou přesností výpočtů. Délka stupnice je pak až několik metrů.
Samotný pojem přesnost může mít více významů. Na jedné straně může znamenat, s jakými tolerancemi byly stupnice na pravítko naneseny. Jak přesně bylo pravítko vyrobeno. Druhým významem, a tím se tady teď budu zabývat, je přesnost výpočtu ve smyslu počtu platných číslic.
Přesnost logaritmického pravítka je dána délkou stupnice. Čím je stupnice delší, tím je možné ji detilněji rozdělit a dosáhnout pak větší přesnosti odečítání hodnot. A když se na logaritmické pravítko podíváte, pochopíte, že možnosti přesného odečítání na levé části pravítka jsou větší, než na pravé. Takže přesnost odečítání pravítka se po délce stupnice mění.
U standardních lineárních pravítek se tak můžeme setkat s následujícími základními délkami:
- 5″ – Pravítko je dlouhé okolo 15 cm, základní C, D stupnice jsou dlouhé asi 12,5 cm. Udávaná přesnost je pak 2 až 3 platné číslice.
- 10″ – Pravítko je dlouhé okolo 30 cm, základní C, D stupnice jsou dlouhé asi 25 cm. Udávaná přesnost je pak asi 3 platné číslice.
- 20″ – Pravítko je dlouhé okolo 60 cm, základní C, D stupnice jsou dlouhé asi 50 cm. Udávaná přesnost je pak 3 až 4 platné číslice.
Pro porovnání velikostí jsou na obrázku logaritmická pravítka firmy Faber Castell systému Rietz, shora – 5″ model 67/87, 10″ model 1/87 a 20″ model 4/87.
I tady však existují vyjímky z pravidla, například 10″ pravítko Faber Castell 2/83N je vybaveno speciálními stupnicemi W1 a W2, které prodlužují efektivní délku pravítka na ekvivalent 20″ a tím umožňují zvětšit přesnost výpočtů.
Kruhová logaritmická pravítka umožňují zvětšit délku základní C a D stupnice. Například u modelu Aristo 623 je délka stupnice 38 cm při průměru pravítka 12 cm.
Ještě delší jsou stupnice u válcových logaritmických pravítek. Například u anglického Otis King je délka stupnice 168cm při relativně kompaktních rozměrech samotného pravítka – délce 17 cm a průměru 4 cm.
U stolního sudového pravítka Nestler 45 je délka stupnice 12,5 m při délce válce 53 cm a průměru 16 cm. Přesnost takovýchto modelů logaritmických pravítek je pak až 5 platných číslic.